Hur fungerar jordplan egentligen del 3

Hur fungerar jordplan egentligen? Del 3. (Publicerat i emc MAGAZINE nr 1, 1999)

Torbjörn Karlsson, Emicon.

I två tidigare nummer av Magazinet har vi studerat hur strömmar bildas på ett jordplan som följd av att en strömförande ledare kommer i närheten. Vi ska nu se vad detta kan ha för effekt på koppling mellan två ledare.

Men först ska vi ta upp en fråga som kommit in från läsekretsen. Det är Jan Carlsson i Mölndal som har påpekat att det finns en paradox gömd i den förra artikeln. Laddningen på en plattledning är beräknad som om ledningen har tjockleken noll, men trots det kan man ändå påstå att det finns en viss laddningsfördelning på ena sidan om ledningen och en annan laddningsfördelning på den andra sidan. Det borde inte vara möjligt att hänföra laddningen till någon speciell sida. Hur kan det komma sig att detta ändå är gjort i artikeln?

Frågeställningen har en ganska djup fysikalisk förklaring som trots det går att uttrycka på ett rätt enkelt sätt. Elektromagnetiska fält och därmed även laddningsfördelningar och strömtätheter lyder väldigt strikta lagar som kan beskrivas med matematiska uttryck. Det är faktiskt så att om man känner strömfördelningen på alla ledare kan man beräkna elektromagnetiska fältstyrkan i alla punkter. Om en ledare med tjockleken noll omges av en fältstyrka som är större på den ena sidan än på den andra, kan man därav dra slutsatsen att strömtätheten är starkast på den sida där fältstyrkan är störst. Det följer av en regel som säger att strömtätheten på en ledares yta har samma amplitud som den tangentiella komponenten av magnetiska fältstyrkan alldeles intill metallytan. Med den metod vi har använt i figurerna för att visa elektriska och magnetiska fält är det lättast att se styrkan hos det elektriska fältet som visas med pilar. Elektriska fältets normalkomponent är proportionell mot laddningstätheten på metallytan. Laddningsfördelningen och strömfördelningen är lika, men ström och laddning är tidsförskjutna så att laddningen blir störst när strömmen är minst och tvärtom.

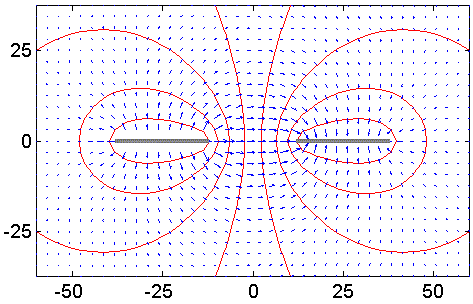
Låt oss nu betrakta vad som händer med två ledare som tillsammans närmar sig ett jordplan. En viktig komponent för kopplingen mellan två ledare är den ömsesidiga kapacitansen, som beskriver den laddning per längdenhet q₁₂, som samlas på vardera ledaren när man lägger en spänning V₁₂ mellan dem. Om man har många ledare brukar man kalla q₁₂/V₁₂ för en delkapacitans. Vi kan beräkna kapacitansen per meter mellan de två plattledningarna i figur 1 genom att summera all beräknad laddning på en ledare och dividera med den pålagda spänningen. I detta fall får vi kapacitansen 13,8 pF/m

Figur 1. Beräknad fältfördelning omkring två plattledningar, som har potentialerna -V/2 respektive +V/2. Avståndet mellan ledarna är en ledarbredd. I figuren är ledarbredden 25 längdenheter, vilka kan väljas fritt eftersom det bara är förhållandena som bestämmer kapacitansen, men vi antar här 25 mm. Elektriskt fält med blå pilar ser en aning osymmetriskt ut eftersom pilarna visar fältstyrkan vid pilarnas fotpunkt. Röda kurvor är ekvipotentiallinjer. Kapacitansen mellan ledarna är 13,8 pF/m.

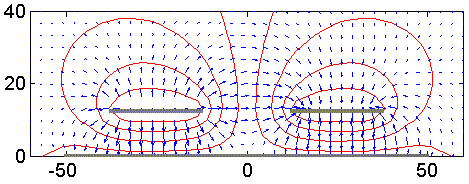
Figur 2. Samma ledare som i figur 1 i närheten av ett jordplan som är 1 dm brett. Fältbilden är starkt påverkad av jordplanet. Avståndet mellan ledare och jordplan är lika med halva ledarbredden. Kapacitiva kopplingen har minskat med 10,6 dB genom att en del av fältlinjerna går via jordplanet.

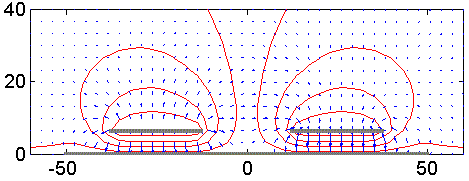
Figur 3. Samma som figur 2 men ännu mindre avstånd, en fjärdedel av ledarbredden, mellan ledare och jordplan. Den kapacitiva kopplingen har minskat ytterligare drygt 3 dB.

De elektriska fältlinjerna går från laddning på den ena ledaren till laddning på den andra ledaren. Ekvipotentiallinjerna på stort avstånd från ledarna bildar cirklar. I figur 2 kan vi se hur fältbilden påverkas när ledarna kommer i närheten av jordplanet. De elektriska fältlinjerna går nu delvis mellan laddningar på ledarna och laddningar på jordplanet. Dessa laddningar bidrar inte till delkapacitansen mellan ledarna vilket är den verksamma kapacitiva kopplingsfaktorn. Delkapacitansen när avståndet är lika med halva ledarbredden, se figur 2, har reducerats till 4,1 pF/m och kapacitiva kopplingen har minskat med 10,6 dB. Mellan jordplanet och varje ledare finns en delkapacitans som är 32 pF/m. Om man mätte kapacitansen mellan plattledarna i ett isolerat system skulle man alltså få 20,1 pF/m. Om man minskar avståndet till jordplanet ytterligare så att det motsvarar en fjärdedel av ledarbredden, som i figur 3, kommer delkapacitansen mellan plattledarena att minska till 2,7 pF/m, vilket ger en minskning av kapacitiva kopplingen med 14 dB med hjälp av jordplanet. I figur 4 kan vi se att kurvan går mot ett värde på y-axeln skilt från 0 när avståndet går mot 0. För avståndet ledarbredden/500 blir det beräknade värdet på delkapacitansen 1 pF/m. De formler som använts här duger inte till att förklara vad som händer på mikroskopiska avstånd men det är rimligt att tänka sig att det finns en viss delkapacitans som beror på laddningarna på plattledningarnas ovansidor ända tills plattorna gör direkt kontakt med jordplanet.

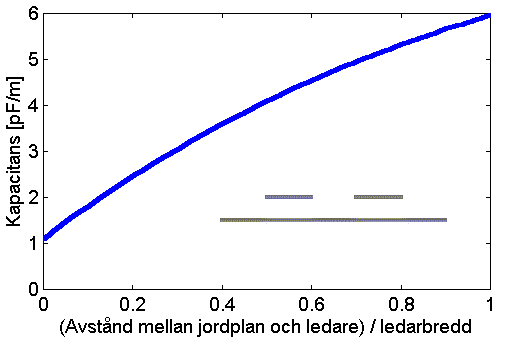
Figur 4. Delkapacitans mellan två plattledningar på olika avstånd från ett jordplan. Plattledningarna är lika och befinner sig på ett avstånd från varandra lika med bredden, se skiss i figuren. Avståndet varierar mellan nästan 0 och en ledningsbredd. Kapacitansen minskar när ledarna närmar sig jordplanet och går mot 1 pF för mycket små avstånd.

Man kan finna mycket intressanta fenomen genom att variera plattledningarnas storlek och läge i förhållande till jordplanet och samtidigt studera hur fältbilden förändras och hur delkapacitanserna varierar. Överhörning mellan ledare bestäms av flera faktorer varav kapacitiva kopplingen, delkapacitansen mellan ledarna, är en. Kapacitansen till jordplanet har också betydelse genom att den påverkar den karakteristiska impedansen. Vi återkommer till andra mekanismer som gör att jordplanet är verksamt i störningsbekämpning . Under tiden kan läsarna studera delkapacitanser för olika ledargeometrier med hjälp av det program som använts för ovanstående beräkningar. Programmet kan hämtas kostnadsfritt från www.emicon.com..