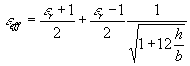
h är ledarens höjd över jordplanet och b är ledarens bredd. Kapacitansen förändras så att Cdiel =
e eff *CluftFormeln gäller för ett dielektriskt skikt med tjocklek h
Länk till: Del 1, Del 2, Del 3, Del 4
Hur fungerar jordplan egentligen?
Del 5. (Publicerat i emc MAGAZINE nr 4, 1999)Torbjörn Karlsson, Emicon
Vi ska den här gången se vilken inverkan ett dielektrikum kan ha på jordplanets funktion. Men efter sommaren kanske det kan vara på sin plats att först göra en liten rekapitulation av tidigare avsnitt. Denna serie började för ett år sedan och det här är den femte delen. För dem som slarvat bort någon tidning kan det vara bra att veta att informationen går att hämta på Internet. På www.Emicon.com finns tidigare artiklar tillsammans med de program som använts för beräkning av kurvor och fältbilder i illustrationerna. Programmen består dels av Matlab-funktioner som kräver att användaren har en relativt sen version av Matlab på sin dator, dels, om det är möjligt, av enkla .exe-filer som kan köras under DOS och som producerar resultat i form av textfiler. Genom att variera indata till programmen kan man göra enkla simuleringar och därmed experimentera fram en praktisk kunskap och förståelse för hur fysiken fungerar.
På vår väg mot svaret på hur jordplan egentligen fungerar har vi hittills fått följande viktiga kunskap:
Låt oss nu ställa frågan: Minskar överhörningen mellan två ledare om vi för dem närmare jordplanet?
Vi tycker kanske rent intuitivt att så borde ske, vad ska annars jordplanet vara bra till. Men som vi tidigare nämnt blir alltså överhörningen obefintlig om man avslutar med karakteristiska impedansen i båda ändar. Om man därefter minskar avståndet till jordplanet ökar överhörningen eftersom karakteristiska impedansen ändras. Nyttan med jordplanet kan sägas vara, att det gör det möjligt att ansluta en riktig avslutning i ledarnas båda ändar.
Nästa fråga inställer sig nu automatiskt: Varför är det då så viktigt med att ledarna ska vara nära jordplanet ?
Jo, om det finns en "utomstående" ledning i närheten som vi inte kan avsluta med karakteristisk impedans är det viktigt att det elektromagnetiska fältet koncentreras kring ledarna så att det inte når fram så mycket energi till den "utomstående" ledaren. Detta åstadkoms genom att avståndet ledare jordplan görs så litet som möjligt.
Det finns ofta dielektriskt material nära ledare och jordplan som kan påverka förhållandena ganska mycket. På kretskort är dielektrikat väl definierat som ett jämntjockt homogent skikt ovanpå jordplanet; i andra sammanhang kan det vara svårt att i detalj veta hur isoleringen omkring exempelvis kablar är konstruerad. En viss kunskap om hur dielektrikum verkar är bra att ha för att förstå hur jordplan fungerar.
Ett dielektriskt material innehåller elektriska laddningar som är bundna av elastiska atomära krafter. Ett neutralt dielektrikum kan beskrivas som en situation där positiva och negativa laddningar sammanfaller helt och neutraliserar varandra på grund av atomära krafter. Dielektrikat påverkas av en yttre positiv elektrisk laddning så att denna attraherar negativa, bundna laddningar och repellerar positiva, bundna laddningar med samma kraft. Man säger att materialet blir polariserat.
Om vi har en ledare med en given potential ovanför ett jordplan och för in en skiva med dielektriskt material mellan ledaren och jordplanet kommer den elektriska fältstyrkan i luften att öka, medan fältstyrkan i skivan blir mindre än vad den var tidigare i luften. Detta innebär att kapacitansen mellan ledare och jordplan ökar och att risken för överslag i området utanför skivan ökar.
Kapacitansen mellan en enkel plattledare och ett jordplan förändras av ett dielektriskt skikt med en faktor som brukar kallas effektiva permittiviteten, vilken kan beskrivas med en ungefärlig formel:
|
|
h är ledarens höjd över jordplanet och b är ledarens bredd. Kapacitansen förändras så att Cdiel = e eff *CluftFormeln gäller för ett dielektriskt skikt med tjocklek h |
Om vi beräknar kapacitanserna för dubbelledningen enligt figur 1 med och utan dielektriskt skikt på jordplanet ska vi se att denna formel är otillräcklig för detta fall.
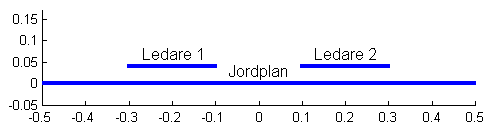
Figur 1.
Dubbelledare över jordplan med förhållande 1:5 mellan höjd och bredd för ledarnaKapacitanserna hos ledningen i figur 1 är 67pF/m mellan ledare och jordplan och 1,24 pF/m mellan ledarna. Med en dielektrisk skiva med e r = 2 mellan ledare och jordplan blir e eff = 1,77 enligt ovanstående formel. Kapacitansen mellan ledare och jordplan blir 119 pF vilket är ungefär 1,77*67 pF, medan kapacitansen mellan ledarna minskar till 1,04 pF . Kapacitansen mellan två plattledare över jordplan med dielektrikum kan alltså inte uppskattas med hjälp av denna formel.
När fältstyrkan i dielektrikat varierar utvecklas värme i materialet av laddningarnas rörelse. Det finns inget förlustfritt dielektriskt material. En elektromagnetisk våg får en reducerad utbredningshastighet i dielektrikum. I vacuum går vågen med hastigheten c0 = 299792500 m/s . I ett dielektrikum med relativ permittivitet e r är hastigheten ![]() .
.
När man studerar överhörning mellan två ledare ovanför ett jordplan tillkommer ytterligare en komplikation om det finns ett dielektriskt skikt på jordplanet. Vågorna på ledarna kommer att gå med två olika hastigheter på grund av dielektrikat. Transmissionsledningen sägs vara inhomogen, eftersom dielektrikat inte är konstant över ledningens tvärsnitt, vilket omfattar hela det område omkring ledarna inom vilket vågutbredningen sker. När flera ledare ingår i en inhomogen transmissionsledning är antalet hastigheter ett mindre än antalet ledare. Detta får till följd att det är omöjligt att göra en perfekt avslutning med obefintlig överhörning.
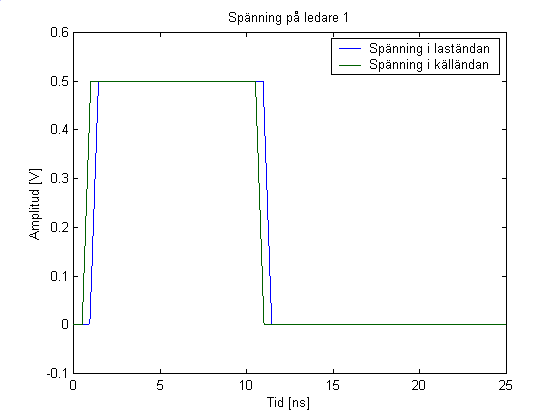
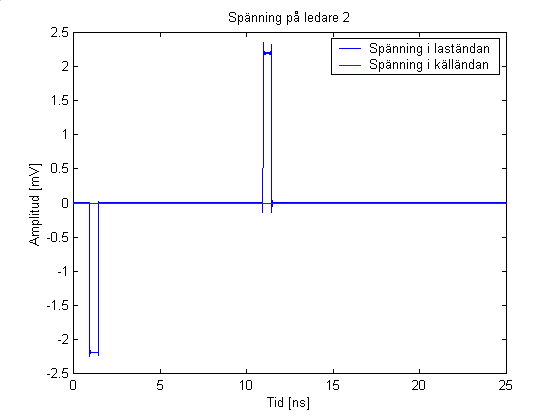
Figur 2
. En spänningspuls med 1 V amplitud matas in på ledning 1, grön kurva överst. En viss överhörning uppstår på ledning 2 i laständan, blå kurva nederst trots att ledningarna är avslutade med den karakteristiska impedansenI figur 2 visas spänningen i båda ändar av en ledning enligt figur 1 med en dielektrisk skiva mellan ledare och jordplan. Ledarna är avslutade i båda ändar med den karakteristiska impedansen. Eftersom det finns vågor med 2 olika hastigheter på ledningen går det som synes inte att bli av med överhörningen fullständigt. Jämför gärna med resultatet i förra delen, i EMC Magazine 3-1999, där spänningen beräknades för en ledning utan dielektrikum. Ladda hem program och experimentera. Skicka gärna synpunkter, kommentarer och frågor till